Last time, we created a calculator prefab with a functional display that allows us to insert expressions on it. However, we are currently unable to evaluate any of these expressions because the equal key does nothing except execute an empty method Display.Evaluate.
public void Evaluate()
{
//TODO: implement in the second part of this tutorial
}Today, we will be building a tokenizer, recursive descent parser, and Abstract Syntax Tree (AST), but first let's take some time to discuss some theory behind these terms to establish a solid foundation.
Tokenization, parsing, and the AST are fundamental components in the construction of a programming language. While our main focus will be creating a basic evaluator for simple mathematical expressions, if you're interested in delving deeper into this subject, I highly recommend a book called "Crafting Interpreters" by Robert Nystrom.
Tokenization, also known as lexical analysis or lexing, is the process of breaking down a sequence of characters or code into smaller units called tokens.
Let's consider an expression like (2.6+4)*8. When our tokenizer receives this string, its output will be a collection of seven tokens: (, 2.6, +, 4, ), *, and 8. Notice the tokenizer's sole responsibility is nothing more than break down the expression into these tokens, without being concerned about the validity or evaluation of the expression.
Now, let's discuss the role of a parser, a recursive descent parser to be exact. You will soon understand why it is named as such when we proceed with its implementation. For now, just note that a recursive descent parser takes in a collection of tokens and outputs an AST.
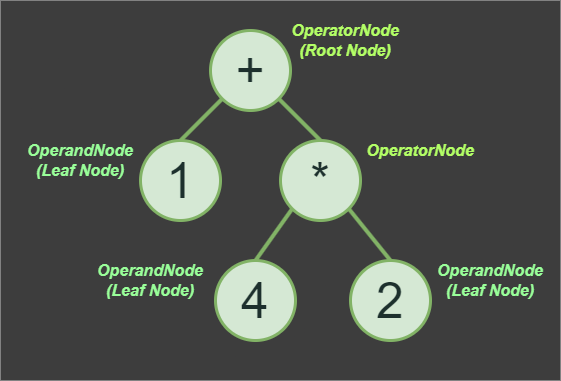
The AST is a hierarchical representation of an expression that captures the relationships between tokens. Like any tree, the AST is a graph, but note that not every graph can be considered a tree.
A graph is a data structure composed of interconnected nodes. Graphs can be classified as directed or undirected, weighted or unweighted, cyclic or acyclic and more.
Sometimes the term vertex is used instead of a node, but in this tutorial, I'm going to stick with the node.
In a tree, each node, except the root node, has a parent node and zero or more child nodes. When a node has no children, it is commonly referred to as a leaf node.
In fact, in this tutorial we're going to work with a special kind of tree, a binary tree, which is a tree where all nodes can have at most two child nodes. We can further divide binary trees to full, complete, perfect, skewed and more.
I won't delve into graph theory here. There are numerous resources that covers this topic much better than I would, like videos by William Fisset. This all is just a very brief overview of the absolute basics without explanations of anything that is not directly relevant to this tutorial.
I highly recommend learning more about graphs and related algorithms. Graph theory consists of one of the most, if not the most, useful concepts in computer science.
There's so much to explore for a curious mind, topics such as Depth-First Search (DFS) and Breadth-First Search (BFS), the Dijkstra, Bellman-Ford, and Floyd-Warshall algorithms, the Traveling Salesman Problem (TSP), finding cycles, bridges, and articulation points and that's only a small fraction.
While learning about graphs, you may find this library I recently wrote in C# solely for educational purposes to be useful. It implements several of the aforementioned algorithms and concepts.
Let's now get back to our parser. Once our parser completes its task of parsing the expression and constructing an AST, it returns the root node of the AST. We then invoke the Evaluate method on this root node, which recursively calls Evaluate on its child nodes. This process continues until the entire tree is evaluated.
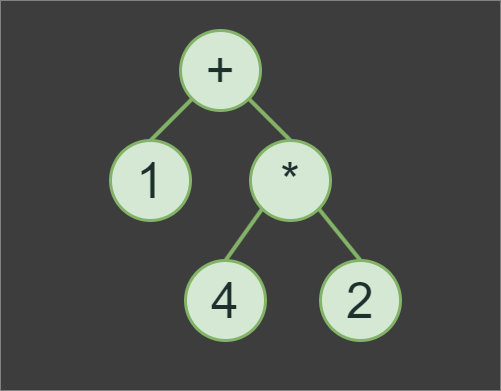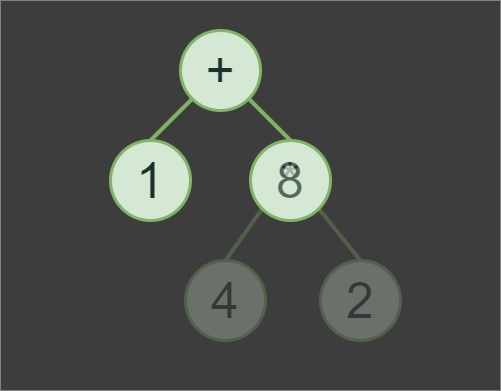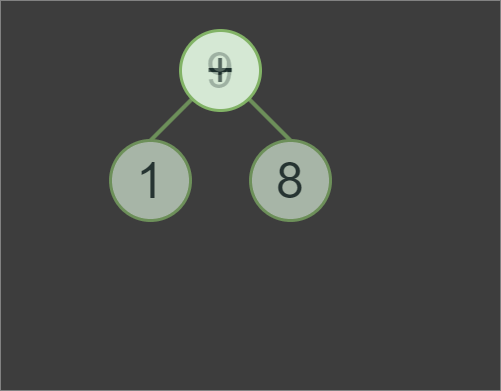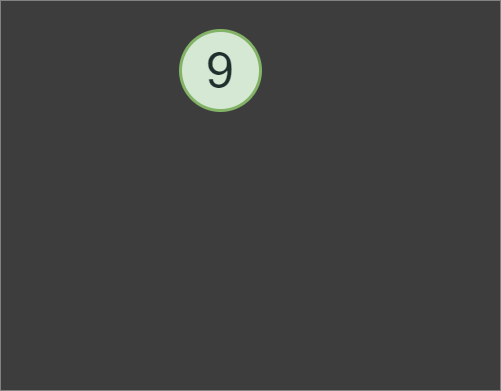
1+4*2, we first evaluates subexpression 4*2 with the result of 8, then 8+1to produce the final result of the expression, which is 9.In addition to implementing the Tokenizer and Parser classes, we also need to implement a Node class. However, the Node class itself will be a very minimalistic pure abstract base class for OperatorNode and OperandNode classes.
Tokenizer
Let's start by implementing a tokenizer. Create a new class in our project, name the file Tokenizer.cs, and type in the following code:
using System.Collections.Generic;
using System.Text;
public static class Tokenizer
{
public static List<string> Tokenize(string expr)
{
List<string> tokens = new();
StringBuilder buffer = new();
foreach (char c in expr)
{
if (c == '+' || c == '/' || c == '*' || c == '-' || c == '(' || c == ')' || c == '^')
{
if (buffer.Length > 0)
{
tokens.Add(buffer.ToString());
buffer.Clear();
}
tokens.Add(c.ToString());
}
else
{
buffer.Append(c);
}
}
if (buffer.Length > 0)
{
tokens.Add(buffer.ToString());
}
return tokens;
}
}The tokenizer starts iterating over characters in the expression If a character is one of the operators (+, -, /, *, (, ), or ^), it adds the operator to the tokens list. However, it also checks if there are any other characters in the buffer, which we utilize a StringBuilder for. If there are, a token is created in the tokens list from the buffer, and the buffer is then cleared.
If a character is not an operator, it must be either a number or a dot. The tokenizer simply appends the character to the buffer. After processing the expression, we check one last time if there are any characters in the buffer. If so, we create a final token using those characters before returning the list of tokens.
Nodes
Before we start implementing a parser, let's first implement a pure abstract Node class and its child classes, OperatorNode and OperandNode. Create a new file named Node.cs, and add in the following code:
using System;
public abstract class Node
{
public abstract double Evaluate();
}Node is a pure abstract class. Such a class consists solely of abstract member functions and does not include any data or concrete member functions.Next, let's add a simple OperandNode class. In the same file, add the following code:
public class OperandNode : Node
{
private readonly double value;
public OperandNode(double value)
{
this.value = value;
}
public override double Evaluate()
{
return value;
}
}OperandNode class is basically a container class for a number, which in our case we internally store as a double.The OperatorNode needs a bit more logic, yet it's still relatively small.
public class OperatorNode : Node
{
private readonly char op;
private readonly Node left;
private readonly Node right;
public OperatorNode(char op, Node left, Node right)
{
this.op = op;
this.left = left;
this.right = right;
}
public override double Evaluate()
{
return op switch
{
'+' => left.Evaluate() + right.Evaluate(),
'-' => left.Evaluate() - right.Evaluate(),
'*' => left.Evaluate() * right.Evaluate(),
'/' => left.Evaluate() / right.Evaluate(),
'^' => Math.Pow(left.Evaluate(), right.Evaluate()),
_ => throw new Exception($"Unknown operator '{op}'"),
};
}
}Evaluate method looks new to you, this is a neat syntactic sugar that came with C# 8.0. It's called switch expression.This is the class that allows the parser to build an AST. Notice how the OperatorNode has a members left and right, both of type Node. Each of these can be either an OperandNode, in which case the Evaluate method simply returns a value, or another OperatorNode, where the Evaluate method traverses down the tree until it reaches a leaf node.
Consider a simple expression, such as 1+2. The corresponding AST would consist of three nodes. The OperatorNode would have a member op of a value + and the OperandNodes assigned as the left and right nodes of the OperatorNode, would have values of 1 and 2, respectively.
Recursive Descent Parser
And finally, the last but also the most significant piece of the puzzle: the implementation of a parser. Let's start by adding a new file named Parser.cs. In that file, add the following code:
using System;
using System.Collections.Generic;
public class Parser
{
private readonly List<string> tokens;
private int pos = 0;
public Parser(List<string> tokens)
{
this.tokens = tokens;
}
}Now, after the constructor, add a public Parse method.
public Node Parse()
{
Node left = ParseSubAdd();
return left;
}return ParseSubAdd();This method does nothing except calling a ParseSubAdd which we still need to implement.
private Node ParseSubAdd()
{
Node left = ParseDivMul();
while (pos < tokens.Count)
{
char op = tokens[pos++][0];
if (op == '+' || op == '-')
{
Node right = ParseDivMul();
left = new OperatorNode(op, left, right);
}
else
{
pos--;
break;
}
}
return left;
}This method is a bit more interesting. We first call ParseDivMul, which we also need to implement, and assign the return value to a new instance of the Node class, which we named left.
Then, we start looping over tokens, and each time we increment the indexer, pos. If a token is a token for addition or subtraction, we call ParseDivMul again and we assign its result to another new instance of the Node class, this time called right.
Then, we reassign the previously created left to a new OperatorNode, where the operator is a + or - token, the left child is the previously created left node, and the right child is the newly created right node.
If the operator is neither + nor -, we decrement our indexer and break out of the loop. Then, we return the left node.
I completely understand if this is a bit confusing. It was confusing for me when I first saw it too. Bear with me, and let's implement the ParseDivMul method. After that, everything will start to become much clearer.
private Node ParseDivMul()
{
Node left = ParseExp();
while (pos < tokens.Count)
{
char op = tokens[pos++][0];
if (op == '*' || op == '/')
{
Node right = ParseExp();
left = new OperatorNode(op, left, right);
}
else
{
pos--;
break;
}
}
return left;
}Aha! We are doing almost the exact same thing, but instead of addition and subtraction, we now care about multiplication and division and where previously we called ParseDivMul, we now calls ParseExp. Let's implement that method as well.
private Node ParseExp()
{
Node left = ParseLeaf();
while (pos < tokens.Count)
{
char op = tokens[pos++][0];
if (op == '^')
{
Node right = ParseLeaf();
left = new OperatorNode(op, left, right);
}
else
{
pos--;
break;
}
}
return left;
}I guess you already see the pattern here and are getting an idea of why this parser is called a recursive descent parser. You probably also know why we call all these methods in this order.
Yes, it's the reverse order of operation precedence! First, we parse addition and subtraction because it has the lowest precedence. Then, we move on to division and multiplication. Finally, we handle exponentiation, which has the highest precedence.
And what about the ParseLeaf method? This one's a little bit special. Let's take a look at that.
private Node ParseLeaf()
{
string token = tokens[pos++];
if (token == "-")
{
Node node = ParseLeaf();
return new OperatorNode(token[0], new OperandNode(0), node);
}
else if (token == "(")
{
Node node = Parse();
if (pos >= tokens.Count || tokens[pos++] != ")")
{
throw new Exception();
}
return node;
}
else
{
double value = double.Parse(token);
return new OperandNode(value);
}
}After we get the next token, we handle unary - in expressions like -3*2. Additionally, we handle brackets because expressions like (2+2)*3 and 2+2*3 need to be parsed into different trees. Let's go over each case.
If the token is -, it represents a unary minus operator. In this case, the method recursively calls itself to parse the expression following the unary minus. It then creates an OperatorNode with the - operator and the parsed expression as the right operand.
If the token is (, it indicates the start of a subexpression within parentheses. The method calls Parse (straight back to beginning). It then verifies that the parentheses are properly closed. If not, it throws an exception. If the parentheses are closed, it returns the parsed subexpression.
If the token is neither - nor (, it represents a numeric value. The method parses the token as a double-precision floating-point number and creates an OperandNode with the parsed value.
The cherry on top of the Display script
Now that we have our Tokenizer, Node classes, and Parser, let's use them in the Display script to finish our Display.Evaluate method. We had previously left it with a TODO comment.
public void Evaluate()
{
string expression = textMesh.text.Replace("E+", "*10^")
.Replace("E-", "*10^-");
List<string> tokens = Tokenizer.Tokenize(expression);
Parser parser = new(tokens);
try
{
Node node = parser.Parse();
string result = node.Evaluate().ToString();
textMesh.text = result;
}
catch (Exception)
{
textMesh.text = "Invalid syntax";
inFaultState = true;
}
lastOpIsEvaluation = true;
}First, we need to replace any E notation in our expression from the display with a scientific notation, as our parser is not built to handle that format. If a result is too large, we can get from double.ToString(); for example 2E+120 which we can append more symbols to create another expression. That's why we need to change it to 2*10^120 which is an equivalent and valid expression for our parser.
Then, we use our Tokenizer to split the expression into tokens, and we feed these tokens to our Parser to obtain a root node. We then call the Evaluate method on the root node and use the ToString method to convert the result into a string that we can display on a TextMesh component.
However, a user might try to evaluate an invalid expression, such as 3+*6. That's why we wrap the evaluation process in a try-catch block. If any exception occurs, we simply display Invalid syntax and set the isFaultState flag to true.
We also set lastOpIsEvaluation to true at the end. This is because we want the backspace key to erase the entire display if it's the first key pressed after evaluation.
We also want to erase the entire display after any key press when it shows "Invalid syntax". The logic for that has been implemented in the previous part of this tutorial.
Now you can enter the Play mode and test if all the logic is implemented correctly. If something doesn't work as expected, compare your implementation with the example project on GitHub.
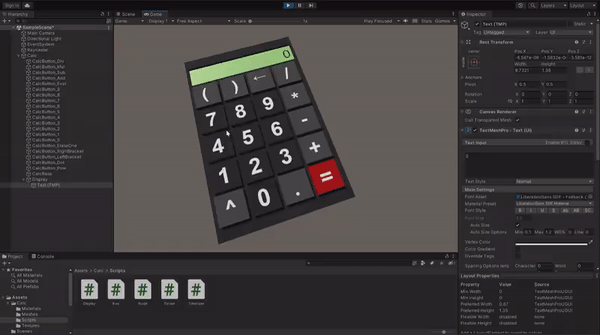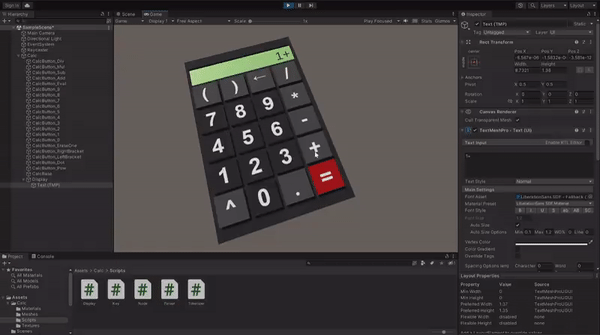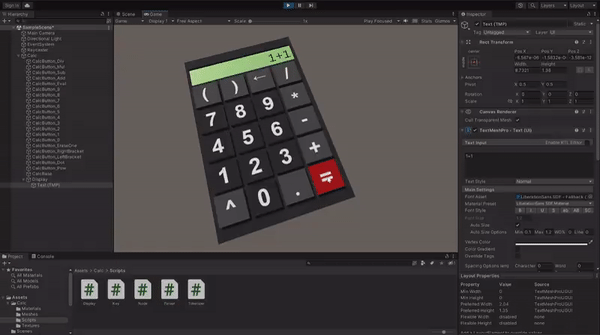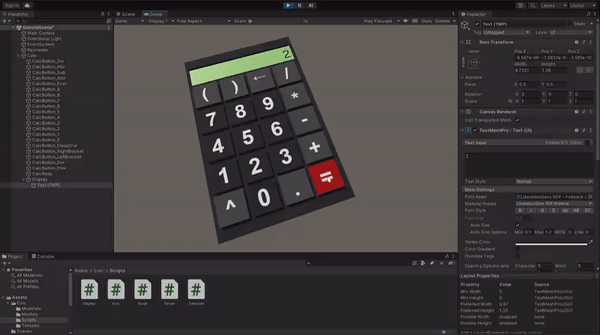
When your calculator is fully functional, drag it from the Hierarchy tab and drop it in Project content tab to to create a prefab.
To VR, or not to VR?
And that's it for the calculator in a non-VR environment. If you're not interested in VR, you don't need to read the third part of this tutorial as it will be focused solely on making the calculator work in VR.
Thank you all for your attention, and for those of you who are interested in VR, see you in the third and the final part of this series and I hope you're enjoying it so far.
If you like my tutorials, follow me on Twitter, where you can find not only more of my tutorials, but also other interesting things related to game development.